Dawkins (1976) considers the following imaginary game. Suppose that the successful raising of an offspring is worth +15 to each parent. The cost of raising an offspring is −20, which can be borne one parent only, or shared equally between two. The cost of a long courtship is −3 to both participants. Females can be ‘coy’ or ‘fast’; males can be ‘faithful’ or ‘philanderer.’ Coy females insist on a long courtship, whereas fast females do not; all females care for offspring they produce. Faithful males are willing, if necessary, to engage in a long courtship, and also care for the offspring. Philanderers are not prepared to engage in a long courtship, and do not care for their offspring. With this assumption, the payoff matrix is shown in Table 23.

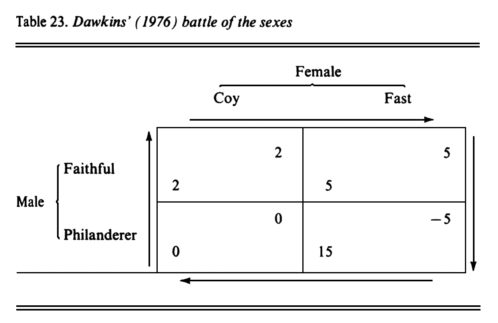
The characteristic feature of this matrix is its cyclical character. That is:

If females are coy, it pays males to be faithful.

If males are faithful, it pays females to be fast.

If females are fast, it pays males to philander.

If males philander, it pays females to be coy.

Thus we have come full circle. The dynamics of such games are discussed in Appendix J. Oscillations are certain, but whether they are divergent or convergent will depend on details of the genetics. If divergent, a population would in practice spend much of its time fixed for a particular pair of strategies. Such a population would be vulnerable to invasion by mutants. Hence, when appropriate mutations occurred it would evolve rather rapidly to a new pair of strategies, and would then again have to wait for new mutations.

Dawkins’ game was an imaginary one. Parker (1979), using explicit genetic models, has suggested that similar cycles could arise from parent-offspring conflict. I am unable to offer illustrative examples, or evidence that such cycles occur. The difficulty is that such cycles, if they occurred, would be of too long a period to be readily observed. Simple models, however, lead so directly to the conclusion that oscillations will occur that it would be wise to be on the lookout for them.